“数”中有思政 “学”中再育人
——《分式方程》第一课时教学设计
字数:2335
2025-09-07
版名:教育理论
□贺 琳
《分式方程》为北京师范大学出版社出版的八年级下册数学教材第五章第四节的内容,分为分式方程的认识、分式方程的解法以及分式方程在实际问题中的应用三个课时,内容由浅入深,是“实际问题—分式方程建模—求解—解释解的合理性”的过程。本章前面三节中陆续介绍了分式、分式的乘除、分式的加减,为本节分式方程学习打下了扎实的基础。
【教学任务】
1.课程性质
分式方程是初中数学“数与代数”领域的重要内容,是一元一次方程的延伸与拓展,是体现“转化思想”“建模思想”的重要载体。
2.思政融合点
通过分式方程的知识建构、问题解决与实际应用,挖掘其中蕴含的科学思维、文化自信、社会责任、社会担当、家国情怀等思政元素,实现知识传授与价值观引领的有机统一。
【教学目标】
让学生理解分式方程的概念,会准确判断分式方程。
让学生能够根据实际问题建立分式方程的数学模型,并能归纳出分式方程的定义;经历观察、比较、归纳分式方程特点的过程,培养逻辑思维。
借助高铁发展、抗震救灾及捐款等实例,激发学生的民族自豪感与社会责任感;引导学生关注社会现象,培养用数学思维解决实际问题的意识,增强学生对数学的热爱。
【教学过程】
第一环节——情境导入
(厚植文化自信)
视频展示宝成铁路及其三条升级线路的发展过程,讲述我国铁路发展史,让学生明确“高铁的发展见证着时代的进步”,引出课题和本节的行程问题。
【设计意图】激发学生的学习兴趣,同时让学生了解祖国交通发展的伟大成就,增强文化自信和民族自豪感。
第二环节——探究新知(培养科学的思维、强化社会责任)
1.出示例题1
甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍。
( 1)你能找出这一问题中的所有等量关系吗?
( 2)如果设特快列车的平均行驶速度为x km/h,那么 x满足怎样的方程?
( 3)如果设小明乘高铁列车从甲地到乙地需yh,那么y 满足怎样的方程?
【设计意图】让学生经历从实际问题抽象、概括分式方程这一“数学化”过程,体会分式方程的模型作用;关键是引导学生努力寻找问题中的所有等量关系,发展学生分析问题、解决问题的能力。
【注意事项】要给学生一定的思考时间,让学生积极投身于问题情境中,引领学生借助思维导图分析问题,找出等量关系,进而顺利列出方程。同时,要注意引导学生理解每一步的实际意义。
2.出示例题2
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款。已知七年级同学捐款总额为4800元,八年级同学捐款总额为5000元,八年级捐款人数比七年级多 20人,而且两个年级人均捐款额恰好相等。如果设七年级捐款人数为x人,那么x满足怎样的方程?
【设计意图】再次让学生经历从实际问题中抽象、概括分式方程这一“数学化”过程,体会分式方程的模型作用。通过捐款问题体现中学生的社会责任、社会担当以及家国情怀。
【注意事项】20分钟的微型课,时间有限,教师借助思维导图带领学生进行分析,有助于更快更准地找出等量关系。
第三环节——感悟升华
(培养科学思维)
1.回顾刚才得出的3个方程
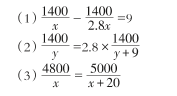
它们和我们以前学过的方程有什么不一样?上面的方程有什么共同特点?
2.引导学生思考,归纳总结
方程中的未知数都含在分母中,不是一元一次方程。这就是我们今天要认识的一种新的方程——分式方程,即分母中含有未知数的方程。
分式方程的重要特征:方程;含分母;分母中含未知数。
分式方程与整式方程的区别:分式方程中分母含有未知数,而整式方程中的分母不含有未知数。
【设计意图】让学生通过观察、归纳、概括出整式方程与分式方程的异同,从而得出分式方程的概念。
第四环节——课堂反馈
找找看,下列方程中哪些是分式方程?
A . 5x + 1/ 2 B . 2(x-2)+1=7
C .3-x /π= 1/2 D . 1/x- 2 =3/x
【设计意图】通过反馈练习,考查学生对分式方程概念的理解。
小结作业
1.总结升华(凝练价值观念)
从今天的课程中,你学到了哪些知识?掌握了哪些方法?
2.作业布置
( 1)巩固性作业:课本习题5.7的1、2、3题。
( 2)拓展性作业:观察身边的现象(如家庭用电、交通时间),尝试用分式方程提出一个问题。
点评
这是一节以学生为中心、重在素养达成的优质学科思政示范课,教师设计精巧,育人无声。设计精巧体现在两个情境驱动,即普快列车和高铁列车对比、灾区重建募捐。
贺老师上了一节课,但也可以说是上了两节课。一节充满探究、充满生成、充满思想(模型思想)的数学课;一节有文化味(中国速度)、有科技味(高铁)、有人情味(募捐)的学科思政课。
本节课的亮点体现在:尊重数学学科本质,以数学逻辑为核心,以思政教育为升华,体现了两个关键词“重构”“模型”。充分利用学生的认知基础和生活经验,结合教材已有情境进行科学整合。
本节课的德育挖掘体现在:“三语”育人,体现充分。课头的引导语结合“徐家坪铁路发展史的今夕对比”视频,激发兴趣、引人思考;课中的衔接语设计精巧,过渡自然;课后的总结语既紧扣主题点题,又升华思想育人。
“情境”育人,润物无声。高铁列车和特快列车的对比,揭示列车速度的变化,是人民生活飞速发展变化的体现;不仅提升民族自信心、自豪感,更是中华民族凝心聚力实现科技发展的有力见证和现实呈现。重建家园,自愿募捐,体现了团结和爱心。
注重思维,突出引导。建立等量关系时,设置层层递进的引导性问题,从纵、横两个方面进行思考。师生互动、生生互动设置有效,充分体现了“数学中,你想到什么不是最重要的,你怎么想的才最关键”。练习设计,兼顾知识容量与思维容量。
模型观念,培育素养。本节课主要发展培养学生的模型观念,在问题解决的过程中,贺老师通过设好“元”(未知数),让学生自主思考,找出等量关系,自主构建方程来解决。
建议引导学生建立等量关系时,把生成式的思考流程图、知识结构图以思维导图的形式呈现,将会更具启发性。
(点评教师:陕西省优秀教学能手邓传锋)
《分式方程》为北京师范大学出版社出版的八年级下册数学教材第五章第四节的内容,分为分式方程的认识、分式方程的解法以及分式方程在实际问题中的应用三个课时,内容由浅入深,是“实际问题—分式方程建模—求解—解释解的合理性”的过程。本章前面三节中陆续介绍了分式、分式的乘除、分式的加减,为本节分式方程学习打下了扎实的基础。
【教学任务】
1.课程性质
分式方程是初中数学“数与代数”领域的重要内容,是一元一次方程的延伸与拓展,是体现“转化思想”“建模思想”的重要载体。
2.思政融合点
通过分式方程的知识建构、问题解决与实际应用,挖掘其中蕴含的科学思维、文化自信、社会责任、社会担当、家国情怀等思政元素,实现知识传授与价值观引领的有机统一。
【教学目标】
让学生理解分式方程的概念,会准确判断分式方程。
让学生能够根据实际问题建立分式方程的数学模型,并能归纳出分式方程的定义;经历观察、比较、归纳分式方程特点的过程,培养逻辑思维。
借助高铁发展、抗震救灾及捐款等实例,激发学生的民族自豪感与社会责任感;引导学生关注社会现象,培养用数学思维解决实际问题的意识,增强学生对数学的热爱。
【教学过程】
第一环节——情境导入
(厚植文化自信)
视频展示宝成铁路及其三条升级线路的发展过程,讲述我国铁路发展史,让学生明确“高铁的发展见证着时代的进步”,引出课题和本节的行程问题。
【设计意图】激发学生的学习兴趣,同时让学生了解祖国交通发展的伟大成就,增强文化自信和民族自豪感。
第二环节——探究新知(培养科学的思维、强化社会责任)
1.出示例题1
甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍。
( 1)你能找出这一问题中的所有等量关系吗?
( 2)如果设特快列车的平均行驶速度为x km/h,那么 x满足怎样的方程?
( 3)如果设小明乘高铁列车从甲地到乙地需yh,那么y 满足怎样的方程?
【设计意图】让学生经历从实际问题抽象、概括分式方程这一“数学化”过程,体会分式方程的模型作用;关键是引导学生努力寻找问题中的所有等量关系,发展学生分析问题、解决问题的能力。
【注意事项】要给学生一定的思考时间,让学生积极投身于问题情境中,引领学生借助思维导图分析问题,找出等量关系,进而顺利列出方程。同时,要注意引导学生理解每一步的实际意义。
2.出示例题2
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款。已知七年级同学捐款总额为4800元,八年级同学捐款总额为5000元,八年级捐款人数比七年级多 20人,而且两个年级人均捐款额恰好相等。如果设七年级捐款人数为x人,那么x满足怎样的方程?
【设计意图】再次让学生经历从实际问题中抽象、概括分式方程这一“数学化”过程,体会分式方程的模型作用。通过捐款问题体现中学生的社会责任、社会担当以及家国情怀。
【注意事项】20分钟的微型课,时间有限,教师借助思维导图带领学生进行分析,有助于更快更准地找出等量关系。
第三环节——感悟升华
(培养科学思维)
1.回顾刚才得出的3个方程
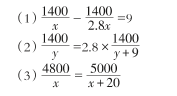
它们和我们以前学过的方程有什么不一样?上面的方程有什么共同特点?
2.引导学生思考,归纳总结
方程中的未知数都含在分母中,不是一元一次方程。这就是我们今天要认识的一种新的方程——分式方程,即分母中含有未知数的方程。
分式方程的重要特征:方程;含分母;分母中含未知数。
分式方程与整式方程的区别:分式方程中分母含有未知数,而整式方程中的分母不含有未知数。
【设计意图】让学生通过观察、归纳、概括出整式方程与分式方程的异同,从而得出分式方程的概念。
第四环节——课堂反馈
找找看,下列方程中哪些是分式方程?
A . 5x + 1/ 2 B . 2(x-2)+1=7
C .3-x /π= 1/2 D . 1/x- 2 =3/x
【设计意图】通过反馈练习,考查学生对分式方程概念的理解。
小结作业
1.总结升华(凝练价值观念)
从今天的课程中,你学到了哪些知识?掌握了哪些方法?
2.作业布置
( 1)巩固性作业:课本习题5.7的1、2、3题。
( 2)拓展性作业:观察身边的现象(如家庭用电、交通时间),尝试用分式方程提出一个问题。
点评
这是一节以学生为中心、重在素养达成的优质学科思政示范课,教师设计精巧,育人无声。设计精巧体现在两个情境驱动,即普快列车和高铁列车对比、灾区重建募捐。
贺老师上了一节课,但也可以说是上了两节课。一节充满探究、充满生成、充满思想(模型思想)的数学课;一节有文化味(中国速度)、有科技味(高铁)、有人情味(募捐)的学科思政课。
本节课的亮点体现在:尊重数学学科本质,以数学逻辑为核心,以思政教育为升华,体现了两个关键词“重构”“模型”。充分利用学生的认知基础和生活经验,结合教材已有情境进行科学整合。
本节课的德育挖掘体现在:“三语”育人,体现充分。课头的引导语结合“徐家坪铁路发展史的今夕对比”视频,激发兴趣、引人思考;课中的衔接语设计精巧,过渡自然;课后的总结语既紧扣主题点题,又升华思想育人。
“情境”育人,润物无声。高铁列车和特快列车的对比,揭示列车速度的变化,是人民生活飞速发展变化的体现;不仅提升民族自信心、自豪感,更是中华民族凝心聚力实现科技发展的有力见证和现实呈现。重建家园,自愿募捐,体现了团结和爱心。
注重思维,突出引导。建立等量关系时,设置层层递进的引导性问题,从纵、横两个方面进行思考。师生互动、生生互动设置有效,充分体现了“数学中,你想到什么不是最重要的,你怎么想的才最关键”。练习设计,兼顾知识容量与思维容量。
模型观念,培育素养。本节课主要发展培养学生的模型观念,在问题解决的过程中,贺老师通过设好“元”(未知数),让学生自主思考,找出等量关系,自主构建方程来解决。
建议引导学生建立等量关系时,把生成式的思考流程图、知识结构图以思维导图的形式呈现,将会更具启发性。
(点评教师:陕西省优秀教学能手邓传锋)